Najnowsze wpisy, strona 1


Macierze
Autor: blodween
19 listopada 2015, 20:17

Macierz – układ liczb, symboli lub wyrażeń zapisanych w postaci prostokątnej tablicy. Choć słowo „macierz” oznacza najczęściej macierz dwuwskaźnikową, to możliwe jest rozpatrywanie macierzy wielowskaźnikowych (zob. notacja wielowskaźnikowa). Macierze jednowskaźnikowe nazywa się często wektorami wierszowymi lub kolumnowymi, co wynika z zastosowań macierzy w algebrze liniowej. W informatyce macierze modeluje się zwykle za pomocą (najczęściej dwuwymiarowych) tablic.

Po więcej informacji zapraszam na:
Macierz- WIKI
Macierz_ikona

ZADANIA
Ark5

Granica funkcji
Autor: blodween
19 listopada 2015, 20:15

 

Granica funkcji – wartość, do której obrazy danej funkcji zbliżają się nieograniczenie dla argumentów dostatecznie bliskich wybranemu punktowi. Funkcjonują dwie równoważne definicje podane przezAugustina Louisa Cauchy'ego oraz Heinricha Eduarda Heinego.

Definicja 1.Punkt x0 jest punktem skupienia zbioru liczbowego X, jeżeli dowolnie blisko x0 znajduje się nieskończenie wiele liczb ze zbioru X.

Definicja 2.Otoczeniem U(x0;r) punktu x0 nazywamy przedział otwarty (x0−r,x0+r) o środku w punkcie x0.
Definicja 3.Punkt x0 jest punktem skupienia zbioru X, jeżeli w dowolnym otoczeniu punktu x0 istnieje nieskończenie wiele wartości z X.


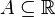
Jeśli funkcje f i g, określone na zbiorze A \subseteq \mathbb R, mają granice właściwe \lim_{x \to x_0}~f(x) = a i \lim_{x \to x_0}~g(x) = b, to:
\lim_{x \to x_0}~(f(x) \pm g(x)) = a \pm b, \lim_{x \to x_0}~(f(x) \cdot g(x)) = a \cdot b, \lim_{x \to x_0}~\tfrac{f(x)}{g(x)} = \tfrac{a}{b}, gdy g(x) \ne 0 oraz b \ne 0.

Całki
Autor: blodween
19 listopada 2015, 20:12

Całka – ogólne określenie wielu różnych, choć powiązanych ze sobą pojęć analizy matematycznej. Najczęściej przez "całkę" rozumie się całkę oznaczoną lubcałkę nieoznaczoną, choć istnieje wiele innych odmian całki. Ścisłe definicje można znaleźć w artykułach dotyczących poszczególnych całek.

W artykule rachunek różniczkowy i całkowy podana jest historia ewolucji znaczenia samego słowa całka. Polskojęzyczny termin został wprowadzony przezJana Śniadeckiego jako tłumaczenie integral

 

Pochodne
Autor: blodween
19 listopada 2015, 20:02

Pochodna – miara szybkości zmian wartości funkcji względem zmian jejargumentów.

 

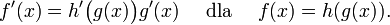iloczyn pochodnej przez stałą, (af)'(x) = af'(x)\; pochodną sumy funkcji (addytywność), (f + g)'(x) = f'(x) + g'(x)\;; pochodną iloczynu funkcji (reguła Leibniza), (fg)'(x) = f'(x) g(x) + f(x) g'(x)\; pochodną złożenia funkcji (reguła łańcuchowa), f'(x) = h'\bigl(g(x)\bigr) g'(x) \quad\text{ dla }\quad f(x) = h(g(x)). pochodną funkcji odwrotnej, \left(f^{-1}\right)'(y) = \bigl(f'(x)\bigr)^{-1}, \quad\text{ o ile }\quad f'(x) \ne 0. pochodną odwrotności funkcji (reguła odwrotności), \left(\tfrac{1}{g(x)}\right)' = \frac{-g'(x)}{g^2(x)}, \quad\text{ o ile }\quad g(x) \ne 0 pochodną ilorazu funkcji (reguła ilorazu), \left(\tfrac{f(x)}{g(x)}\right)' = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}, \quad\text{ o ile }\quad g(x) \ne 0

 

Literatura:

Korn G. A., Korn T. M.: Matematyka dla pracowników naukowych i inżynierów. T. 1. PWN, 1983. Kuratowski K.: Rachunek różniczkowy i całkowy. Funkcje jednej zmiennej. PWN, 1967. Бугров Я. С., Никольский С. М.: Дифференциальное и интегральное исчисление. Наука, 1984. Kane J. W., Sternheim M. M.: Fizyka dla przyrodników. T. 2. PWN, 1988. Прохоров Ю. В., Розанов Ю. А.: Теория вероятностей. Наука, 1987.
Wykład z analizy matematycznej
Autor: blodween
19 listopada 2015, 19:55