Granica funkcji
19 listopada 2015, 20:15
Granica funkcji – wartość, do której obrazy danej funkcji zbliżają się nieograniczenie dla argumentów dostatecznie bliskich wybranemu punktowi. Funkcjonują dwie równoważne definicje podane przezAugustina Louisa Cauchy'ego oraz Heinricha Eduarda Heinego.
Definicja 1.Punkt x0 jest punktem skupienia zbioru liczbowego X, jeżeli dowolnie blisko x0 znajduje się nieskończenie wiele liczb ze zbioru X.
Definicja 2.Otoczeniem U(x0;r) punktu x0 nazywamy przedział otwarty (x0−r,x0+r) o środku w punkcie x0.
Definicja 3.Punkt x0 jest punktem skupienia zbioru X, jeżeli w dowolnym otoczeniu punktu x0 istnieje nieskończenie wiele wartości z X.
Jeśli funkcje i
i  , określone na zbiorze
, określone na zbiorze 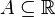 , mają granice właściwe
, mają granice właściwe  i
i  , to:
, to:


 gdy
gdy  oraz
oraz 
Definicja 1.Punkt x0 jest punktem skupienia zbioru liczbowego X, jeżeli dowolnie blisko x0 znajduje się nieskończenie wiele liczb ze zbioru X.
Definicja 2.Otoczeniem U(x0;r) punktu x0 nazywamy przedział otwarty (x0−r,x0+r) o środku w punkcie x0.
Definicja 3.Punkt x0 jest punktem skupienia zbioru X, jeżeli w dowolnym otoczeniu punktu x0 istnieje nieskończenie wiele wartości z X.
Jeśli funkcje
 i
i  , określone na zbiorze
, określone na zbiorze 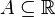 , mają granice właściwe
, mają granice właściwe  i
i  , to:
, to:

 gdy
gdy  oraz
oraz 

Dodaj komentarz