Pochodne
19 listopada 2015, 20:02
Pochodna – miara szybkości zmian wartości funkcji względem zmian jejargumentów.
iloczyn pochodnej przez stałą,
 pochodną sumy funkcji (addytywność),
pochodną sumy funkcji (addytywność),
 ;
pochodną iloczynu funkcji (reguła Leibniza),
;
pochodną iloczynu funkcji (reguła Leibniza),
 pochodną złożenia funkcji (reguła łańcuchowa),
pochodną złożenia funkcji (reguła łańcuchowa),
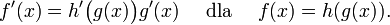 pochodną funkcji odwrotnej,
pochodną funkcji odwrotnej,
 pochodną odwrotności funkcji (reguła odwrotności),
pochodną odwrotności funkcji (reguła odwrotności),
 pochodną ilorazu funkcji (reguła ilorazu),
pochodną ilorazu funkcji (reguła ilorazu),

Dodaj komentarz