Archiwum listopad 2015, strona 1


Całki
Autor: blodween
19 listopada 2015, 20:12

Całka – ogólne określenie wielu różnych, choć powiązanych ze sobą pojęć analizy matematycznej. Najczęściej przez "całkę" rozumie się całkę oznaczoną lubcałkę nieoznaczoną, choć istnieje wiele innych odmian całki. Ścisłe definicje można znaleźć w artykułach dotyczących poszczególnych całek.

W artykule rachunek różniczkowy i całkowy podana jest historia ewolucji znaczenia samego słowa całka. Polskojęzyczny termin został wprowadzony przezJana Śniadeckiego jako tłumaczenie integral

 

Pochodne
Autor: blodween
19 listopada 2015, 20:02

Pochodna – miara szybkości zmian wartości funkcji względem zmian jejargumentów.

 

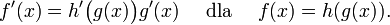iloczyn pochodnej przez stałą, (af)'(x) = af'(x)\; pochodną sumy funkcji (addytywność), (f + g)'(x) = f'(x) + g'(x)\;; pochodną iloczynu funkcji (reguła Leibniza), (fg)'(x) = f'(x) g(x) + f(x) g'(x)\; pochodną złożenia funkcji (reguła łańcuchowa), f'(x) = h'\bigl(g(x)\bigr) g'(x) \quad\text{ dla }\quad f(x) = h(g(x)). pochodną funkcji odwrotnej, \left(f^{-1}\right)'(y) = \bigl(f'(x)\bigr)^{-1}, \quad\text{ o ile }\quad f'(x) \ne 0. pochodną odwrotności funkcji (reguła odwrotności), \left(\tfrac{1}{g(x)}\right)' = \frac{-g'(x)}{g^2(x)}, \quad\text{ o ile }\quad g(x) \ne 0 pochodną ilorazu funkcji (reguła ilorazu), \left(\tfrac{f(x)}{g(x)}\right)' = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}, \quad\text{ o ile }\quad g(x) \ne 0

 

Literatura:

Korn G. A., Korn T. M.: Matematyka dla pracowników naukowych i inżynierów. T. 1. PWN, 1983. Kuratowski K.: Rachunek różniczkowy i całkowy. Funkcje jednej zmiennej. PWN, 1967. Бугров Я. С., Никольский С. М.: Дифференциальное и интегральное исчисление. Наука, 1984. Kane J. W., Sternheim M. M.: Fizyka dla przyrodników. T. 2. PWN, 1988. Прохоров Ю. В., Розанов Ю. А.: Теория вероятностей. Наука, 1987.
Wykład z analizy matematycznej
Autor: blodween
19 listopada 2015, 19:55

Strony do nauki
Autor: blodween
19 listopada 2015, 19:28
Algebra liniowa
Autor: blodween
19 listopada 2015, 19:25
Algebra liniowa – dział algebry zajmujący się badaniem przestrzeni liniowych oraz ich homomorfizmów, tj. przekształceń liniowych. Algebra liniowa skupia się głównie na badaniu przestrzeni skończenie wymiarowych nad ciałami lub ogólniej,pierścieniami. Do algebry liniowej można zaliczyć także teorię form kwadratowych, macierzy, przekształceń półtora- iwieloliniowych. Dziedzina ta wyrosła w sposób naturalny na gruncie badania układów równań liniowych.
Algebra liniowa ma liczne zastosowania zarówno w matematyce (np. równania różniczkowe, programowanie liniowe), jak i poza nią, np. w ekonomii metody przez nią wypracowane są stosowane do skutecznego modelowania i rozwiązywania problemów związanych z alokacją zasobów.
 
 

Literatura:

Grzegorz Banaszak, Wojciech Gajda: Elementy algebry liniowej Tom 1 i 2, Wydawnictwo Naukowo-Techniczne 2002 Andrzej Białynicki-Birula: Algebra liniowa z geometrią, PWN, Warszawa 1979 Aleksiej I. Kostrykin: Wstęp do algebry: Algebra liniowa, PWN, Warszawa 2004 Andrzej Mostowski, Marceli Stark: Algebra liniowa, PWN, Warszawa 1968 Jacek Gancarzewicz: Algebra liniowa i jej zastosowania, UJ, Kraków 2009