Algebra Banacha, Analiza matematyczna

Algebra Banacha – przestrzeń Banacha z określonym dodatkowym działaniem mnożenia wraz z którym tworzy algebrę nad ciałem liczb rzeczywistych bądź zespolonych oraz spełnia warunek

$\x\cdot y\ \leqslant \x\ \y\$

dla wszystkich jej elementów $x,y$ . Definicja ta ma również sens dla przestrzeni unormowanych, które niekoniecznie sązupełne – w takim przypadku mówi się o algebrach unormowanych. Jeżeli działanie mnożenia jest przemienne to mówi się odpowiednio o przemiennych algebrach unormowanych i przemiennych algebrach Banacha.

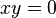W ogólnym przypadku, algebra nad ciałem liczb zespolonych może nie mieć jedynki – skrajnym przykładem jest dowolnaprzestrzeń liniowa $A$ z mnożeniem określonym wzorem $xy = 0$ dla dowolnych $x, y \in A$ (jeżeli $A$ jest przestrzenią Banacha, to jest ona przykładem algebry Banacha, w której jedynka nie może być aproksymowana – tzn. nie istnieje ciąg $(e_n)_{n\in \mathbb{N}}$ o wyrazach z przestrzeni A o tej własności, że $\e_n\=1$ dla każdej liczby naturalnej n oraz

$\lim_{n \to \infty}~\e_n \cdot a - a\ = \lim_{n\to\infty}~\a \cdot e_n - a\ = 0,\; a\in A$ .

Pojęcie algebry Banacha wprowadził w 1936 roku Mitio Nagumo[1].

Analiza matematyczna

Strona główna

Algebra Banacha

Dodaj komentarz