Najnowsze wpisy


Algebra Banacha
Autor: blodween
04 grudnia 2015, 18:01

Algebra Banacha – przestrzeń Banacha z określonym dodatkowym działaniem mnożenia wraz z którym tworzy algebrę nad ciałem liczb rzeczywistych bądź zespolonych oraz spełnia warunek

\x\cdot y\ \leqslant \x\ \y\

dla wszystkich jej elementów x,y. Definicja ta ma również sens dla przestrzeni unormowanych, które niekoniecznie sązupełne – w takim przypadku mówi się o algebrach unormowanych. Jeżeli działanie mnożenia jest przemienne to mówi się odpowiednio o przemiennych algebrach unormowanych i przemiennych algebrach Banacha.

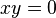W ogólnym przypadku, algebra nad ciałem liczb zespolonych może nie mieć jedynki – skrajnym przykładem jest dowolnaprzestrzeń liniowa A z mnożeniem określonym wzorem xy = 0 dla dowolnych x, y \in A (jeżeli A jest przestrzenią Banacha, to jest ona przykładem algebry Banacha, w której jedynka nie może być aproksymowana – tzn. nie istnieje ciąg (e_n)_{n\in \mathbb{N}} o wyrazach z przestrzeni A o tej własności, że \e_n\=1 dla każdej liczby naturalnej n oraz

\lim_{n \to \infty}~\e_n \cdot a - a\ = \lim_{n\to\infty}~\a \cdot e_n - a\ = 0,\; a\in A.

Pojęcie algebry Banacha wprowadził w 1936 roku Mitio Nagumo[1].

Własności wyznaczników
Autor: blodween
04 grudnia 2015, 17:58

- wyznacznik macierzy transponowanej jest równy wyznacznikowi macierzy wyjściowej,
- jeżeli macierz posiada wiersz zerowy (kolumnę zerową), wówczas detA = 0,
- jeżeli macierz posiada dwa identyczne wiersze (kolumny), wówczas detA = 0,
- jeżeli jakiś wiersz (kolumna) jest kombinacją liniową innych wierszy (kolumn), wówczas detA = 0,
- zamiana miejscami dwóch wierszy lub dwóch kolumn macierzy powoduje zmianę znaku wyznacznika,
- jeżeli w danej macierzy elementy danego wiersza lub kolumny zostaną przemnożone przez dowolną liczbę k ≠ 0, wówczas wartość wyznacznika również zostanie przemnożona przez k,
- zachodzi równość det(A · B) = detA · detB

Blogi innych studentów
Autor: blodween
19 listopada 2015, 20:27

Układ równań liniowych
Autor: blodween
19 listopada 2015, 20:23

Układ równań liniowych – koniunkcja pewnej liczby (być może nieskończonej)równań liniowych, czyli równań pierwszego rzędu.
Teoria układów równań liniowych jest działem algebry liniowej leżącej u podstaw nowoczesnej matematyki. Algorytmami obliczeniowymi zajmuje się dział nazywany numeryczna algebra liniowa, same zaś metody odgrywają ważną rolę w inżynierii,fizyce, chemii, informatyce i ekonomii. Częstokroć aproksymuje (przybliża) się bardziej skomplikowane układy równań nieliniowych (opisujące modele matematyczne, czy symulacje komputerowe) dużo prostszymi układami równań liniowych (tzw. linearyzacja).
Układy równań liniowych rozpatruje się najczęściej nad ciałami (np. liczbami wymiernymi, rzeczywistymi, czy zespolonymi); choć ma to sens już w przypadkupierścieni (np. liczb całkowitych), to rozwiązywanie takich układów nastręcza znacznie więcej trudności (w szczególności oznacza to badanie modułów zamiast przestrzeni liniowych, zob. uogólnienia). W dalszej części przyjmuje się, że wszystkie współczynniki należą do ustalonego ciała.

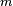Niech \scriptstyle \mathrm U oznacza układ \scriptstyle m równań liniowych o \scriptstyle n niewiadomych, tzn.

\mathrm U\colon \begin{cases}\begin{matrix} a_{11} x_1 & + & a_{12} x_2 & + & \dots & + & a_{1n} x_n & = b_1, \\ a_{21} x_1 & + & a_{22} x_2 & + & \dots & + & a_{2n} x_n & = b_2, \\ \vdots & & \vdots & & \ddots & & \vdots & \vdots \\ a_{m1} x_1 & + & a_{m2} x_2 & + & \dots & + & a_{mn} x_n & = b_m. \end{matrix}\end{cases}

Niech \scriptstyle 1 \leqslant i \leqslant m oraz \scriptstyle 1 \leqslant j \leqslant n. Wielkości \scriptstyle x_j nazywa się niewiadomymi (lub zmiennymi), liczby \scriptstyle a_{ij} nazywa się współczynnikami, zaś elementy \scriptstyle b_i to wyrazy wolne. Układ nazywa się jednorodnym, jeżeli wyrazy wolne są równe zeru; inaczej mówiąc, wszystkie równania jednorodnego układu równań liniowych są jednorodne.

Układ \scriptstyle \mathrm U można zapisać jako równanie wektorowe

[x_1 a_{11} + \dots + x_n a_{1n},\ \dots,\ x_1 a_{m1} + \dots + x_n a_{mn}] = [b_1, \dots, b_m],

które można przedstawić w postaci

x_1[a_{11}, \dots, a_{m1}] + \dots + x_n[a_{1n}, \dots, a_{mn}] = [b_1, \dots, b_m],

dzięki czemu każda niewiadoma może być postrzegana jako współczynnik kombinacji liniowej wektorów \scriptstyle \mathbf a_j = [a_{1j}, \dots, a_{mj}], tzn.

x_1 \mathbf a_1 + x_2 \mathbf a_2 + \dots + x_n \mathbf a_n = \mathbf b,

gdzie \scriptstyle \mathbf b = [b_1, b_2, \dots, b_m] nazywa się w tym kontekście wektorem wyrazów wolnych, zaś \scriptstyle \mathbf x = [x_1, x_2, \dots, x_n] to wektor zmiennych (zob. uogólnienia).

Korzystając z notacji macierzowej układ \scriptstyle \mathrm U można przedstawić w postaci

\begin{bmatrix} a_{11} x_1 & + & a_{12} x_2 & + & \dots & + & a_{1n} x_n \\ a_{21} x_1 & + & a_{22} x_2 & + & \dots & + & a_{2n} x_n \\ \vdots & & \vdots & & \ddots & & \vdots \\ a_{m1} x_1 & + & a_{m2} x_2 & + & \dots & + & a_{mn} x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix},

co, przy pomocy standardowego mnożenia macierzy, można zapisać w formie

\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix}.


Innymi słowy dowolny układ \scriptstyle \mathrm U można traktować jak macierzowe równanie liniowe

Test - Granica i ciągłość funkcji
Autor: blodween
19 listopada 2015, 20:20
Funkcja \displaystyle \displaystyle f\colon\bigg[-\frac{\pi}{2},\frac{\pi}{2}\bigg]\longrightarrow \mathbb{R} określona wzorem \displaystyle \displaystyle f(x)= \left\{ \begin{array} {lll} \displaystyle \frac{x}{\sin x} & \textrm{dla} & x\neq 0\\ 1 & \textrm{dla} & x=0 \end{array} \right.
 jest ciągła dla wszystkich \displaystyle \displaystyle x\in\bigg[-\frac{\pi}{2},\frac{\pi}{2}\bigg] Dobrze
 jest ciągła w \displaystyle x=0 Dobrze
 nie jest ciągła
 

Granica \displaystyle \displaystyle\lim_{x\to 0}(1+3x^2)^{\frac{1}{x^2}} jest równa
 \displaystyle 0
 \displaystyle 1
 \displaystyle e^3 Dobrze
 

Dana jest funkcja \displaystyle f:\mathbb{R}\to\mathbb{R} ciągła i taka, że \displaystyle f(1)0 i \displaystyle f(2)0. Wtedy prawdą jest, że
 funkcja \displaystyle f nie ma pierwiastków w przedziale \displaystyle \displaystyle [1,2]
 funkcja \displaystyle f może mieć dokładnie jeden pierwiastek w przedziale \displaystyle \displaystyle [1,2] Dobrze
 funkcja \displaystyle f może mieć więcej niż jeden pierwiastek w przedziale \displaystyle \displaystyle [1,2] Dobrze
 

Funkcja \displaystyle \displaystyle f(x)=\frac{\sin x}{x} w nieskończoności
 ma granicę równą \displaystyle 1
 ma granicę równą \displaystyle 0 Dobrze
 nie ma granicy
 

Niech \displaystyle \displaystyle a=\lim_{x\to 0^+}e^{-\frac{1}{x}},\displaystyle b=\lim_{x\to 0^-}e^{-\frac{1}{x}}. Wtedy
 \displaystyle a=0,\displaystyle b=+\infty Dobrze
 \displaystyle a=0,\displaystyle b=-\infty
 \displaystyle a=+\infty,\displaystyle b=+\infty
 

Granica \displaystyle \displaystyle\lim_{x\to 0}\frac{\ln(1+x^3)}{x^3} jest równa
 \displaystyle +\infty
 \displaystyle 0
 \displaystyle 1 Dobrze